
 |
| ||
|
|
 |
This Document | ||||
 | |||||
 |
SummaryPlus |  |
|||
 |
Full Text + Links |  |
|||
 |
·Thumbnail Images |  |
|||
 |
PDF (448 K) |  |
|||
 | |||||
 |
Actions | ||||
 | |||||
 |
Cited By | ||||
 |
Save as Citation Alert | ||||
 |
E-mail Article | ||||
 |
Export Citation | ||||
 |
|||||
Robust position-based routing for wireless ad hoc networks
Kousha Moaveninejad ,
,
 ,
Wen-Zhan Song
,
Wen-Zhan Song and
Xiang-Yang Li
and
Xiang-Yang Li
Department of Computer Science, Illinois
Institute of Technology, Chicago, IL 60616, United States
Available
online 15 September 2004.
We consider a wireless ad hoc network composed of a set of wireless nodes
distributed in a two dimensional plane. Several routing protocols based on the
positions of the mobile hosts have been proposed in the literature. A typical
assumption in these protocols is that all wireless nodes have uniform
transmission regions modeled by unit disk centered at each wireless node.
However, all these protocols are likely to fail if the transmission ranges of
the mobile hosts vary due to natural or man-made obstacles or weather
conditions. These protocols may fail because either some connections that are
used by routing protocols do not exist, which effectively results in
disconnecting the network, or the use of some connections causes livelocks. In
this paper, we describe a robust routing protocol that tolerates up to roughly
40% of variation in the transmission ranges of the mobile hosts. More precisely,
our protocol guarantees message delivery in a connected ad hoc network whenever
the ratio of the maximum transmission range to the minimum transmission range is
at most ![]() .
.
Keywords: Localized routing; Planar structure; Wireless ad
hoc networks ![]()
Recent years saw a great amount of research in wireless networks, especially ad hoc wireless networks due to its potential applications in various situations such as battlefield, emergency relief, and so on. One of the key challenges in the design of ad hoc networks is the development of dynamic routing protocols that can efficiently find routes between two communication nodes. In recent years, a variety of routing protocols [6], [16], [17], [18], [19] and [22] targeted specifically for ad hoc environment have been developed. The routing protocols proposed may be categorized as table-driven protocols or demand-driven protocols. Table-driven routing protocols maintain up-to-date routing information between every pair of nodes. The changes to the topology are maintained by propagating updates of the topology throughout the network. Source-Initiated On-Demand Routing creates routes only when desired by the source node. At this time a route discovery process is initiated within the network. For the review of the state of the art of routing protocols, see surveys by Royer and Toh [21] and by Ramanathan and Steenstrup [20]. Route discovery can be very expensive in communications costs, reducing the response time of the network. On the other hand explicit route maintenance can be even more costly in the explicit communication of substantial routing information.
Recently, many researchers have proposed the use of location information to reduce the amount of control traffic. Ko and Vaidya [10] essentially use the DSR protocol, but suggest that a node forwards a packet to a node only if it is in a request zone which is likely to contain a path to the desired destination. The DREAM protocol [2] uses a limited flooding of data packets. On the other hand, another set of greedy-based routing protocols, which completely stay away from the flooding paradigm and every node selects the next node to forward the packets based on the information in the packet header, and the position of its local neighbors, were proposed recently. This neighbor is selected by locally optimizing some criteria such as the length of the path to the destination, or the direction difference between the target and the neighbor.
Let s be the source node, t be the destination node, and
u be the current node u that has the packet and will decide which
node to forward the packets. In Compass Routing [11],
node u finds the next relay node v such that the angle 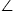 vut
is the smallest among all neighbors of u in a given topology. A variation
called Random Compass Routing is also proposed in [11].
In Greedy Routing [4],
node u finds the next relay node v such that the distance
vut
is the smallest among all neighbors of u in a given topology. A variation
called Random Compass Routing is also proposed in [11].
In Greedy Routing [4],
node u finds the next relay node v such that the distance  vt
vt is the smallest
among all neighbors of u in a given topology. In Most Forwarding
Routing [23],
node u finds the next relay node v such that
is the smallest
among all neighbors of u in a given topology. In Most Forwarding
Routing [23],
node u finds the next relay node v such that  v′t
v′t is the smallest
among all neighbors of u in a given topology, where v′ is the
projection of v on segment ut. In Farthest Neighbor Routing
node u finds the farthest node v as forwarding node among all
neighbors of u in a given topology such that
is the smallest
among all neighbors of u in a given topology, where v′ is the
projection of v on segment ut. In Farthest Neighbor Routing
node u finds the farthest node v as forwarding node among all
neighbors of u in a given topology such that 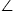 vut
vut 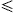 α. Here
angle α is a parameter, which is less than π/2 typically. Another
variation is Nearest Neighbor Routing: node u finds the nearest
node v as forwarding node among all neighbors of u in a given
topology such that
α. Here
angle α is a parameter, which is less than π/2 typically. Another
variation is Nearest Neighbor Routing: node u finds the nearest
node v as forwarding node among all neighbors of u in a given
topology such that 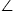 vut
vut 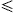 α.
Notice that it is shown in [4]
and [11]
that the compass routing, random compass routing and the greedy routing
guarantee to deliver the packets from the source to the destination if Delaunay
triangulation is used as network topology. Here a network topology G over
a set V of wireless nodes is Delaunay triangulation if the circumcircle
of every triangle uvw (with uv, uw, wv in G)
does not contain any node from V inside. However, it is expensive to
construct Delaunay triangulation in a distributed manner. Obviously, there are
several scenarios in which greedy routing fails if Delaunay triangulation is not
used. We proposed a structure called local Delaunay triangulation [15]
to approximate the Delaunay triangulation. The proof that these localized
routing protocols guaranteeing delivery does not hold anymore in this local
Delaunay triangulation, although in most cases, these greedy routing protocols
do work on local Delaunay triangulation.
α.
Notice that it is shown in [4]
and [11]
that the compass routing, random compass routing and the greedy routing
guarantee to deliver the packets from the source to the destination if Delaunay
triangulation is used as network topology. Here a network topology G over
a set V of wireless nodes is Delaunay triangulation if the circumcircle
of every triangle uvw (with uv, uw, wv in G)
does not contain any node from V inside. However, it is expensive to
construct Delaunay triangulation in a distributed manner. Obviously, there are
several scenarios in which greedy routing fails if Delaunay triangulation is not
used. We proposed a structure called local Delaunay triangulation [15]
to approximate the Delaunay triangulation. The proof that these localized
routing protocols guaranteeing delivery does not hold anymore in this local
Delaunay triangulation, although in most cases, these greedy routing protocols
do work on local Delaunay triangulation.
To overcome the failure of all these greedy-based routing strategies, several
researchers proposed another set of localized routing protocols which basically
use the right-hand rule to guarantee the delivery of the packets. A
planar network topology that can be constructed efficiently in a
distributed manner is required for the success of all localized routing
protocol. Lin et al. [23]
proposed the first localized algorithm that guarantees delivery by memorizing
past traffic at nodes. Bose et al. [4]
proposed to use the Gabriel graph as underlying structure for the Face routing method. Subsequently, Karp et al. [7]
discussed in detail of medium access layer and conducted experiments with moving
nodes for Face routing method. Barriére et al. [1]
extended the scheme on graphs which are fuzzy unit graphs, that is, two nodes
are connected if their distance is at most r, not connected if the
distance is at least R, and may be connected otherwise. They showed that
their algorithm works correctly if ![]() . Routing according to the right-hand rule, which
guarantees delivery in planar graphs [3],
is also used when simple greedy-based routing heuristics fail.
. Routing according to the right-hand rule, which
guarantees delivery in planar graphs [3],
is also used when simple greedy-based routing heuristics fail.
All previous methods (except [1])
assumed that all wireless nodes have the same transmission range, and a node
u can receive the message from another node v as long as the
distance between them is less than the uniform global transmission range.
Consequently, all wireless nodes V together define a unit disk graph
UDG(V), which has an edge uv if and only if the Euclidean
distance  uv
uv between u and v is less than one unit. Several planar
structures (such as RNG, GG) have been proposed to be used as the underlying
network topology of UDG for localized routing protocols that guarantee the
packets delivery.
between u and v is less than one unit. Several planar
structures (such as RNG, GG) have been proposed to be used as the underlying
network topology of UDG for localized routing protocols that guarantee the
packets delivery.
However, graphs representing communication links are rarely so completely
specified as the unit disk graphs. We thus consider the general structure of
arbitrary graphs defined by points in the plane, geometric graphs. For
example, for wireless communications, different nodes may have different
transmission radius. Consequently, two nodes can communicate directly if they
are within the transmission range of each other, i.e., there is a communication
link between these two nodes. The graph formed by all such communication links
is different from the traditional disk graph, in which two nodes are connected
by a straight edge if the two corresponding disks centered at these two nodes
intersect. And for wireless communications, two nodes sometimes cannot
communicate directly even though they are within the transmission range of each
other, due to the blocking of the signal by some barrier. Hereafter, we call the
graph, formed by all wireless nodes and the edges uv representing that
two nodes u and v can communicate directly, the communication
graph. Let ru be the transmission range of a node
u. A communication graph is then called mutual communication graph
(MG), when there is an edge uv iff  uv
uv
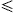 min{ru, rv}.
min{ru, rv}.
It is easy to construct a configuration of a set of nodes (their positions and transmission ranges) such that there is no planar subgraph of the original communication graph when nodes have different transmission ranges and some links may be missing due to the blocking of signal. We thus have to rely on some virtual links to build a planar structure. It is nature to request that we use as less virtual links as possible.
In this paper, we present a new method of constructing planar topologies for communication graphs that is not UDG. Our simulations show a significant improvement of messages used by our method compared with the previous method without lossing the routing performance.
The rest of the paper is organized as follows. In Section 2, we discuss in detail of the network model used in this paper and review some previous results on robust position-based routing for this model. We present our method in Section 3. In Section 4, we study the performance of our method compared with the previous method. We conclude our paper in Section 5.
We consider a wireless ad hoc network (or sensor network) with all nodes distributed in a two-dimensional plane. Assume that all wireless nodes have distinctive identities and each static wireless node knows its position information1 either through a low-power Global Position System (GPS) receiver or through some other way. By one-hop broadcasting, each node u can send its location information to all nodes within the transmission region of u. Throughout this paper, a broadcast by a node u means u sends the message to all nodes within its transmission region.
In wireless ad hoc networks, the transmission region of a node u is defined as the locations where the radio signal sent out by the node u can be recognized by the receiver node. For simplicity, it is traditionally assumed that the transmission region of each wireless node is a disk with unit radius. Here a disk centered at a node u with radius ru, denoted by D(u, ru), is the set of points whose distance to u is at most ru. Thus all nodes together define a unit disk graph as communication graph. However, graphs representing communication links are rarely so completely specified as the unit disk graph. Different nodes may have different transmission radius, and more importantly, the transmission region of a node is never as perfect as a disk. Considering this imperfect transmission region, previous routing algorithms, which guarantee the packet delivery using some planar subgraph as network topology, are likely to fail since the difficulty of constructing a planar subgraph from the communication graph and some links may be missing. In the worst case, the communication graph could be very complicated. To have some meaningful study, we assume that each node u has a maximum transmission radius Ru and a minimum transmission radius ru. These two thresholds depend on both the environment and the mobile hosts’ technology. Thus, the transmission region of a node u (the region where nodes can receive the transmission by u) is contained inside disk D(u, Ru) and contains the disk D(u, ru). See Fig. 1 for an illustration. Thus, two mobile hosts u and v cannot communicate directly (that is, exchange messages) if their Euclidean distance exceeds the value min(Ru, Rv). Conversely, two mobile hosts are always mutually reachable if their Euclidean distance is below the value min(ru, rv).
Fig. 1. The transmission region of a node is modelled by a quasi-disk.
The network is then represented by a geometric undirected graph,
G = (V, E), with vertices representing
mobile hosts, and edges representing communication links. The set of vertices
V is thus a set of points in the Euclidean plane. Let  uv
uv be the Euclidean
distance between the points u and v in the plane. The set of edges
E satisfies {uv
be the Euclidean
distance between the points u and v in the plane. The set of edges
E satisfies {uv u, v
u, v  V,
V,  uv
uv
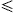 min{ru, rv}}
min{ru, rv}} 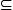 E and E
E and E 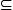 {uv
{uv u, v
u, v 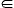 V,
V,  uv
uv
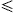 min{Ru, Rv}}.
The nodes corresponding to the mobile hosts, and the edges between a mobile host
and its neighbors form the graph G. Two mobile hosts u and
v with
min{ru, rv}
min{Ru, Rv}}.
The nodes corresponding to the mobile hosts, and the edges between a mobile host
and its neighbors form the graph G. Two mobile hosts u and
v with
min{ru, rv} 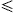
 uv
uv
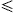 min{Ru, Rv}
may or may not be able to communicate directly.
min{Ru, Rv}
may or may not be able to communicate directly.
More precisely, let R(u) be the transmission region of a node
u, i.e., from where other nodes can receive the signal sent by u.
Then our assumption is that R(u) is contained inside the disk
D(u, Ru) and contains the disk
D(u, ru). Two nodes u and
v can communicate directly iff they are inside the transmission region of
each other. Let I(u) be all nodes that can send signal to
u, i.e., I(u) = {v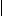 u
u 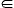 R(v)}. Let T(u) be all nodes that can
receive signal from u, i.e., T(u) = {v
R(v)}. Let T(u) be all nodes that can
receive signal from u, i.e., T(u) = {v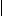 v
v 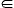 R(u)}. Let N(u) be the neighbors of
u in G, i.e.,
N(u) = I(u) ∩ T(u).
R(u)}. Let N(u) be the neighbors of
u in G, i.e.,
N(u) = I(u) ∩ T(u).
We note that the transmission conditions do not vary rapidly with time, compared to the speed of electronic communications. This implies that the network may change, for example, due to a change in the weather conditions, but it is at a time scale that allows an easy resetting of the network. Thus, we assume from now on that the connections between mobile hosts are fixed. However, the structure of these connections is not known, and it is the role of our protocol to ensure message delivery in this unknown network.
Modeling the transmission region by a quasi-disk is not our innovation:
Barriŕre et al. [1]
has also applied this model. They assumed, in addition, that the radius
Ru is the same (say all nodes have value R) for
all nodes u, and ru has the same value r.
They gave a three-phase protocol that guarantees the delivery of the packet as
long as ![]() . The central part of their protocol is a
construction of a planar structure in a distributed manner. Since the original
communicate graph may not contain a planar subgraph at all, it uses some
virtual links. To distinguish the created virtual links from others, we
call the communication links in the original graph as actual links. It
defines the virtual links using a recursive approach: given any link uv
(could be virtual or actual), if there is a node w inside the disk
disk(u, v), then add links uw and vw to
virtual links if they are not actual links. It is easy to show that all virtual
links have length at most R by induction. Since
. The central part of their protocol is a
construction of a planar structure in a distributed manner. Since the original
communicate graph may not contain a planar subgraph at all, it uses some
virtual links. To distinguish the created virtual links from others, we
call the communication links in the original graph as actual links. It
defines the virtual links using a recursive approach: given any link uv
(could be virtual or actual), if there is a node w inside the disk
disk(u, v), then add links uw and vw to
virtual links if they are not actual links. It is easy to show that all virtual
links have length at most R by induction. Since ![]() , obviously, one of the links of uw and
vw must have length at most
, obviously, one of the links of uw and
vw must have length at most ![]() , i.e., it is an actual link in the communication
graph. After collecting all virtual links, the algorithm then applies the
Gabriel structure to the new graph (with all actual links and virtual links). A
simple proof can show that the final structure is a connected planar graph.
, i.e., it is an actual link in the communication
graph. After collecting all virtual links, the algorithm then applies the
Gabriel structure to the new graph (with all actual links and virtual links). A
simple proof can show that the final structure is a connected planar graph.
However, although the virtual links are necessary for constructing a planar
structure, their protocol creates many unnecessary virtual links. They also gave
an example, which shows that it creates many such unnecessary virtual links even
the original communication graph is already a planar structure.2
Fig.
2 illustrates such an example. There are 2n nodes: n nodes
u1, u2, …, un
are equally distributed on the left segment; n nodes
v1, v2, …, vn
are equally distributed on the right segment. They are placed such that 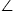 uiui+1vi = π/2,
uiui+1vi = π/2,
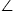 uivi+1vi = π/2,
in addition to u1v1 = R and
unvn = r +
uivi+1vi = π/2,
in addition to u1v1 = R and
unvn = r +  for an arbitrarily small positive real number
for an arbitrarily small positive real number  . A simple execution of their protocol shows that the final planar
structure has all links
uiui+1,
vivi+1, (1
. A simple execution of their protocol shows that the final planar
structure has all links
uiui+1,
vivi+1, (1 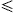 i
i 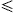 n − 1) and
unvn (but no link
u1v1). Notice that the original
communication graph has link u1v1 instead of
the virtual link unvn. The
shortest path connecting u1 and v1 in this
final planar structure has length
n − 1) and
unvn (but no link
u1v1). Notice that the original
communication graph has link u1v1 instead of
the virtual link unvn. The
shortest path connecting u1 and v1 in this
final planar structure has length ![]() . There are O(n) unnecessary virtual links
uivi + 1 and
ui + 1vi created.
Notice the original communication graph is already a planar structure.
. There are O(n) unnecessary virtual links
uivi + 1 and
ui + 1vi created.
Notice the original communication graph is already a planar structure.
Fig. 2. Excessive virtual links are created (then removed in left case).
If we let the nodes ui and ui + 1 (so do vi and vi + 1) arbitrarily close, then their protocol will add all edges uivj as virtual links. Thus, in the worst case, it could add O(n2) unnecessary virtual links and then remove all these virtual links (except unvn) even the original communication graph is planar. The right figure of Fig. 2 shows that their method adds O(n) virtual links to the final structure even it is unnecessary. In this paper, we present a new method to construct a planar structure that is more efficient in terms of communications and power spanning ratio without creating excessive virtual links.
Before we discuss our method, we first review some definitions that will be
used later. For any pair of nodes u and v, let
lune(u, v) be the intersection of two disks centered
at u and v with radius  uv
uv and disk(u, v) be the disk with diameter
uv. Let disk(u, v, w) be the
circumcircle of a triangle
and disk(u, v) be the disk with diameter
uv. Let disk(u, v, w) be the
circumcircle of a triangle 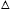 uvw. The
relative neighborhood graph [24],
denoted by RNG(V), consists of all edges uv such that
lune(u, v) is empty of other nodes inside. The
Gabriel graph [5]
GG(V) contains all edges uv such that
disk(u, v) is empty of other nodes. Assume no four
vertices of V are co-circular. The Delaunay triangulation, denoted
by Del(V), is the union of all triangles
uvw. The
relative neighborhood graph [24],
denoted by RNG(V), consists of all edges uv such that
lune(u, v) is empty of other nodes inside. The
Gabriel graph [5]
GG(V) contains all edges uv such that
disk(u, v) is empty of other nodes. Assume no four
vertices of V are co-circular. The Delaunay triangulation, denoted
by Del(V), is the union of all triangles 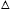 uvw such that
disk(u, v, w) is empty of other nodes.
Obviously, RNG(V)
uvw such that
disk(u, v, w) is empty of other nodes.
Obviously, RNG(V) 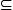 GG(V)
GG(V) 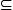 Del(V). Recently, we [15]
also define a sequence of structure called localized Delaunay. A triangle
Del(V). Recently, we [15]
also define a sequence of structure called localized Delaunay. A triangle 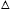 uvw in UDG is called a k-localized Delaunay
triangle if disk(u, v, w) does not
contain any vertex that is within k hops of u, v, or
w. The k-localized Delaunay graph over V, denoted by
LDel(k)(V), has exactly all Gabriel edges in UDG
and edges of all k-localized Delaunay triangles.
uvw in UDG is called a k-localized Delaunay
triangle if disk(u, v, w) does not
contain any vertex that is within k hops of u, v, or
w. The k-localized Delaunay graph over V, denoted by
LDel(k)(V), has exactly all Gabriel edges in UDG
and edges of all k-localized Delaunay triangles.
In this paper, we will use the network model used by Barriŕre et al. [1],
i.e., all nodes have the same radius Ru, say R,
and all nodes have same ru, say r, and ![]() .
.
Our routing scheme consists of five phases: the Link Collecting phase, the Gabriel phase, the Virtual-link Adding phase, the Extraction phase, and the Routing phase. In the Link Collecting phase, each node u will collect all actual links uv, i.e., u and v can communicate mutually and directly. The aim of the Gabriel phase is to remove some edges so the number of intersections processed in the Virtual-link Adding phase decreases, The aim of the Virtual-link Adding phase is to add some edges (called virtual edges) to the physical communication graph to guarantee the connectivity of the graph after the Extraction phase is executed. In other words the Extraction phase might disconnect the graph if we do not add virtual edges. The aim of the extraction phase is to remove the intersections from the physical communication graph and produce a planar graph. Once the extraction phase is done, the routing phase performs message delivery between mobile hosts. All computations in all phases are local and do not require any central controller.
The Gabriel phase and the Virtual-link Adding phase are new contributions, and will be described in detail. The routing phase is basically the same as the routing phase in [4] and [7], and alternates greedy routing with perimeter routing, i.e., routing around the faces of a planar graph using the right-hand rule. Thus we include only a brief discussion of the routing phase.
The following data structures and messages are used by our method:
(1) Data Structures:
(a) N(u) = (bDeleted, bActual, bProcessed, (v, vx, vy), (w, wx, wy)): the history/final (actual or virtual) neighbor list of u where v is ever or now a neighbor of u and w is the relay node if link uv is virtual; bDeleted is a flag to show whether it was ever deleted or not; bActual is a flag to show whether it is an actual edge or a virtual edge; bProcessed is a flag to show whether it was ever processed or not. Initially, all flags are False. If the neighbor is an actual neighbor then the last argument, which is the ID and coordinate of the relay node, would have no meaning.
(b) L(u) = (bDeleted, bProcessed, (v, vx, vy), (w, wx, wy)): the set of all known edges vw by u, where neither v nor w is u. Here bDeleted is a flag to show whether it was ever deleted or not; bProcessed is a flag to show whether it was ever processed or not. Initially, all flags are False.
(2) Message Format:
(a) NewNode(v, vx, vy): a node uses this message to inform other node the information of a node v. Here (vx, vy) is the coordinate of node v.
(b) Confirm(u, v): node u confirms node v that u can receive signal from v.
(c) NewLink(u, v, (ux, uy), (vx, vy)): a node uses this message to inform other node the existence of a link uv. Here uv could be an actual link or a virtual link.
(d) CreateLink(u, v, (ux, uy), (vx, vy)): a node uses this message to inform either node u or node v to create a virtual link uv.
Before we start the Gabriel Phase we have to construct the FUDG graph, so each node will be aware of its neighbors, as follows. Initially, every mobile host broadcasts its own geometry position to the mobile hosts within its transmission region. Unlike the unit disk graph model, knowing the geometry position of another mobile host v, a mobile host u cannot determine whether it can communicate directly with the mobile host v. It only knows that it can receive the message from v, but is not sure whether v can receive its signal. Thus, node u has to send a message Confirm to confirm that it can receive the message from v.
1. Initially, each node u sets an empty neighbor list N(u) and an empty link list L(u). Each node u broadcasts its location information, by sending message NewNode(u,ux,uy) to all nodes inside its transmission region using a local broadcast model.
2. When a node v receives the message NewNode(u, ux,uy) from a node u,
(a) if  uv
uv > r then node v confirms node u
by sending the message Confirm((v,vx,vy),u).
> r then node v confirms node u
by sending the message Confirm((v,vx,vy),u).
(b) if  uv
uv
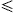 r
then node v adds the record (NotDeleted, Actual,
NotProcessed,
(u,ux,uy),
(null, null, null)) to N(v).
r
then node v adds the record (NotDeleted, Actual,
NotProcessed,
(u,ux,uy),
(null, null, null)) to N(v).
3. If a node u receives a confirmation message Confirm((v, vx, vy), u) from a node v, node u adds the record (NotDeleted, Actual, NotProcessed, (v, vx, vy), (null, null, null)) to N(u).
Now each node has the information of its one-hop neighbors. It then can continue to the next phase. Notice that, node u does not have to wait to collect all its one hop neighbors to start the Gabriel phase. It can perform Gabriel phase whenever it gets the information about a new neighbor. To avoid unnecessary recalculation of the Gabriel Phase, we set a timeout value TMax, which is the time it will start the Gabriel phase after getting the confirmation message from its first neighbor.
We then show that the link information collected by all nodes are consistent:
if node u has a link uv, then node v will also have a link
vu and vice versa. If  uv
uv
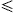 r, then
u and v is for sure that link uv exists and no confirmation
is needed. Otherwise, when node u has a link uv, it means that the
query message sent by u is received by v and the confirmation
message from v is received by u. Consequently, the query message
from v will be received by u and the confirmation message by
u will be received by v. Thus, node v will also create an
actual link vu.
r, then
u and v is for sure that link uv exists and no confirmation
is needed. Otherwise, when node u has a link uv, it means that the
query message sent by u is received by v and the confirmation
message from v is received by u. Consequently, the query message
from v will be received by u and the confirmation message by
u will be received by v. Thus, node v will also create an
actual link vu.
The aim of this phase is to remove some unnecessary links from FUDG graph.
This is performed by extracting the Gabriel graph of FUDG graph with a
slight modification. The unit disk graph, defined on all nodes when assuming
their transmission ranges are r, is a subgraph of FUDG graph. We use
UDG(FUDG) to denote such unit disk graph. The Gabriel Phase removes all the
edges that do not belong to GG(UDG(FUDG)). In other words each edge uv
with length less than r is removed if there exists a node w such
that 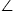 uwv
uwv 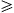 π/2. Removing
edge uv is performed by setting the flag bDeleted of node u
to be True in the adjacency list of node v and
vice versa. These edges will be removed in the Extraction Phase, if we do not
remove them before the Extraction Phase starts. We remove them at this stage so
we will have less number of intersections in the Virtual-link Adding Phase.
π/2. Removing
edge uv is performed by setting the flag bDeleted of node u
to be True in the adjacency list of node v and
vice versa. These edges will be removed in the Extraction Phase, if we do not
remove them before the Extraction Phase starts. We remove them at this stage so
we will have less number of intersections in the Virtual-link Adding Phase.
Then, each node, say u, sends out the information of its neighbors,
say v, whose bDeleted flag is False by
sending the message NewLink((u, ux, uy), (v, vx, vy)).
When a node, say w, which is neither u nor v, receives
NewLink((u, ux, uy), (v, vx, vy)),
and if (a) the link uv does not belong to L(w) and (b) either  uw
uw
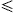 r or
r or
 vw
vw
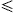 r, then
it adds the record (NotDeleted, NotProcessed,
(u, ux, uy), (v, vx, vy))
to L(w).
r, then
it adds the record (NotDeleted, NotProcessed,
(u, ux, uy), (v, vx, vy))
to L(w).
Notice that, after the Gabriel phase, we only have two sets of links (1) a subset of links with length at most r, and these links form a planar graph (not necessarily connected). (2) all actual links that have length larger than r, but no more than R (these links may intersect themselves or with the links from the first subset). Our next phase will add virtual links so we can remove intersections later.
Consider any two intersected links xy and uv. Either of these
two links could be a virtual link or an actual link. The basic approach of our
method to remove the intersection without disconnecting the network is based on
the following observation illustrated by Fig.
3. Assume 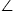 xuy is the largest angle of the quadrilateral. Then we can
remove link xy and add link xu (if it is not added before) to
remove this intersection and preserve the connectivity. If the added link
xu causes the new intersections, we continue to process the new
intersections.
xuy is the largest angle of the quadrilateral. Then we can
remove link xy and add link xu (if it is not added before) to
remove this intersection and preserve the connectivity. If the added link
xu causes the new intersections, we continue to process the new
intersections.
Fig. 3. Two intersected links: one will be removed.
Notice that if we actually remove link xy from the graph immediately, we may end up generating many messages due to the following phenomena: link xy could be added back when we process some other intersections, and then link xy will cause new intersections again (although we have processed it before). To avoid this loop of intersection processing, we will only mark edge xy as deleted but do not actually remove it from the graph now. Later, when processing some other intersections that cause adding a link xy, we first check if link xy exists or not (it could be marked as deleted). If it exists, we do nothing; otherwise, we add the link information to node x and node y.
Since any pair of nodes with distance at most r can communicate directly, the added virtual links have length larger than r. We also prove that all introduced virtual links have length at most R.
Lemma 1
All introduced virtual links have length at most R.
Proof
We prove this by induction on the time of the virtual link introduced to the
structure. When the first virtual link are introduced, all links have length at
most R. The virtual link is introduced since there are two previous known
links intersect each other. Consider any two intersected links uv and
xy. See Fig.
3 for an illustration. The largest angle among the four corner angles 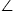 xuy,
xuy, 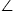 uyv,
uyv, 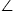 yvx
and
yvx
and 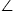 vxu is at least π/2 from the pigeonhole principal. Assume that
vxu is at least π/2 from the pigeonhole principal. Assume that
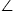 xuy is the largest angle (ties are broken by the largest apex
node ID). Obviously, the shortest edge of xu and uy is at most
xuy is the largest angle (ties are broken by the largest apex
node ID). Obviously, the shortest edge of xu and uy is at most ![]() . W.l.o.g., assume that
. W.l.o.g., assume that  uy
uy
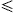
 ux
ux . Consequently, node
u and y can receive the message from each other. Then node
u will know the existence of link xy through node y and
node y will know the existence of link uv through node u.
Then according to our algorithm, node y will decide to remove link
xy and proposes to add links xu and uy (actually uy
already existed as an actual link, thus only link xu could be a virtual
link introduced). Obviously, the length if link xu is less than that of
xy, which is at most R.
. Consequently, node
u and y can receive the message from each other. Then node
u will know the existence of link xy through node y and
node y will know the existence of link uv through node u.
Then according to our algorithm, node y will decide to remove link
xy and proposes to add links xu and uy (actually uy
already existed as an actual link, thus only link xu could be a virtual
link introduced). Obviously, the length if link xu is less than that of
xy, which is at most R.
When links xy, or uv, or both could be virtual links, by
induction, the virtual links introduced from their intersection has length at
most R also. This finishes the proof. 
We then discuss in detail our method of adding virtual links. First of all,
consider any two intersected links, say uv and xy, in the current
configuration of the network. See Fig.
3 for an illustration. W.l.o.g., assume that 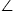 xuy is the
largest angle of the quadrilateral xuyv (ties are broken by ID of the
apex). Then it is easy to show that either uy or ux has length at
most r, i.e., it is an actual link. Assume that
xuy is the
largest angle of the quadrilateral xuyv (ties are broken by ID of the
apex). Then it is easy to show that either uy or ux has length at
most r, i.e., it is an actual link. Assume that  uy
uy
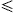 r.
Consequently, both u and y can detect such intersection since they
know the existence of these two links uv and xy (node u
knows xy through node y and node y knows uv through
node u). To avoid that both of them process this intersection, we only
let node u (with the largest angle
r.
Consequently, both u and y can detect such intersection since they
know the existence of these two links uv and xy (node u
knows xy through node y and node y knows uv through
node u). To avoid that both of them process this intersection, we only
let node u (with the largest angle 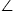 xuy) process
it. Thus, we have the following procedure of adding virtual links.
xuy) process
it. Thus, we have the following procedure of adding virtual links.
1. Assume that node u creates a new link uv. Node u checks whether link uv causes intersections with some links stored in list L(u). If it does cause intersection, say with a link xy, it goes to Step 3.
2. Assume node u receives NewLink(u, v, (xx, xy), (yx, yy)) from some neighbor. Node u checks whether link xy causes intersections with some links stored in list N(u). If it does cause intersection, say with a link uv, goes to Step 3.
3. Node u checks if the following conditions are satisfied: (1) 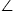 xuy is the largest among the quadrilateral xuyv, and
(2) link ux does not exist. If the conditions are satisfied, node
u will add virtual link ux, i.e., adds record
(notDeleted, notProcessed,
(x, xx, xy), (y, yx, yy))
to L(u).
xuy is the largest among the quadrilateral xuyv, and
(2) link ux does not exist. If the conditions are satisfied, node
u will add virtual link ux, i.e., adds record
(notDeleted, notProcessed,
(x, xx, xy), (y, yx, yy))
to L(u).
Notice that node y can also detect this intersection. Node y then sends a message to node x (through the relay of some other nodes if link yx is virtual) asking it to form a virtual link ux. Node y also marks link xy deleted, i.e., set bDeleted of link xy to True.
When node x receives the message of forming virtual link xu from node y, node x adds node u to its list N(u) and marks link xy deleted also.
Notice that here link xy could be virtual link also. The communication through link xy will then through the relay of a sequence of actual links. In addition, since we check whether the link ux exists or not before we decide to add this link, all added virtual links have length at least r.
This phase is very similar to the Gabriel phase but with some differences. Edges whose length are greater than r might be removed but edges whose length are smaller than r will not be removed. Remember that after the Gabriel phase, we only have two set of edges: (1) edges in GG(UDG(FUDG)) forming a planar graph and with length at most r, and (2) all edges in the original communication graph with length in (r, R]. In the virtual-link adding phase, we only add virtual links with length larger than r. The Extraction phase works as follows:
1. Each node u checks every link uv whose flag
bDeleted is False and  uv
uv > r to see if there is another neighbor w
such that
> r to see if there is another neighbor w
such that 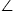 uwv
uwv 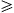 π/2 and link
vw exists. If it has, then set the flag bDeleted of link
uv to be True.
π/2 and link
vw exists. If it has, then set the flag bDeleted of link
uv to be True.
2. All edges whose flag bDeleted are False form the final structure.
In the remainder of the section, we show that our algorithm does terminate and generate a planar structure.
We first show that the final structure is indeed a connected planar graph.
First of all, if the original communication graph is a connected planar graph,
our algorithm will not add any virtual links. The final structure is just
the original communication graph. If the algorithm terminates with two
intersected links, say xy and uv, then according to the proof of
Lemma
1, we know that this intersection will be detected by at least two of these
four nodes x, y, u, and v (in our proof, we show
that u and y will detect the intersection by assuming the 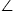 xuy
is the largest angle among the quadrilateral xuyv). We also showed that
one of the nodes will decide to add virtual links (nodes u and x
will add virtual link ux in our assumption). Thus link xy will be
removed in the Extraction phase according to our algorithm. Thus, if the
algorithm terminates, there are no intersected links. It is obvious that the
final structure is connected if the original communication graph is connected
since, everytime when we decide to remove a link that causes intersection, we
already added some virtual links (if necessary) to form a path connecting the
two end-points of the removed link. In addition, the final structure is
connected since we remove an edge uv iff we have links uw and
wv exist (although either of them could be a virtual link).
xuy
is the largest angle among the quadrilateral xuyv). We also showed that
one of the nodes will decide to add virtual links (nodes u and x
will add virtual link ux in our assumption). Thus link xy will be
removed in the Extraction phase according to our algorithm. Thus, if the
algorithm terminates, there are no intersected links. It is obvious that the
final structure is connected if the original communication graph is connected
since, everytime when we decide to remove a link that causes intersection, we
already added some virtual links (if necessary) to form a path connecting the
two end-points of the removed link. In addition, the final structure is
connected since we remove an edge uv iff we have links uw and
wv exist (although either of them could be a virtual link).
We then show that our algorithm does terminate. Notice that although we divide our algorithm to many phases, we do not have to strictly follow these phases, i.e., different nodes may be in different phases, and some node may come back to some earlier phase when necessary. For example, the Virtual-link Adding phase and the Extraction Phase can be interleaved.
We show that the total edge length of the structure is decreased whenever we process an intersected pair of links. Again, assume that intersected links xy and uv are processed. Similar to the proof of Lemma 1, we know that the removed link (edge xy in our proof) has length larger than the possibly added virtual link (edge xu in our proof). Notice that, when we remove a link, it is possible that we do not have to add any virtual link (when xu is already actual link). Since there are at most n2/2 links in a n-node network, the number of connected graphs is also a finite number. Thus, our algorithm is guaranteed to terminate.
After a planar structure is constructed, we then apply some previously developed routing protocols on top of this structure. For completeness, we review some localized routing protocols that rely on a planar structure.
Right-hand rule is long-known method for traversing a graph (in analogy to following the right-hand wall in a maze). And it has been used in some wireless routing protocols [4], [23], [9] and [8]. The rule states that when arriving at node x from node y, the next edge traversed is the next one sequentially counterclockwise about x from edge xy. In the example shown in Fig. 4, x will forward the packet to z following right-hand rule, traversing face P. It is known that the right-hand rule traverses the interior of a closed polygonal region (a face) in clockwise edge order. And it traverses an exterior region in counterclockwise edge order. In general, right-hand rule is applied in planar graphs (in which no edges intersect each other). In [8] a no-crossing heuristic is given to deal with the case where edges cross.
Fig. 4. An illustration of the face routing algorithm.
Applying the right-hand rule in planar graphs, a routing protocol called Face Routing is proposed by [11] (in the paper they call the algorithm Compass Routing II). We consider a planar graph G. The nodes and edges of graph G partition the Euclidean plane into contiguous regions called the faces of G. The main idea of the face routing is to walk along the faces which are intersected by the line segment st between the source s and the destination t. In each face, it uses the right-hand rule to explore the boundaries. On its way around a face, the algorithm keeps track of the points where it crosses the line st. Having completely surrounded a face, the algorithm returns to one of these intersections lying closest to t, where it proceeds by exploring the next face closer to t. Fig. 4 gives an illustration. See [11] and [13] for detailed algorithms. They also proved that the face routing algorithm guarantees to reach the destination t after traversing at most O(n) edges where n is the number of nodes.
Though face routing terminates in linear time, it is not satisfactory, since already a very simple flooding algorithm will terminate in O(n) steps. Then in [13], Kuhn et al. proposed a new method called Adaptive Face Routing (AFR), in which, restricted search areas are used to avoid exploring the complete boundary of faces. The idea is as follows. The exploration of faces is restricted to an ellipse area. The ellipse size is set to an initial estimate of the optimal path length. If face routing fails to reach the destination (when it reaches the ellipse, it has to turn back), the algorithm will restart with a bounding ellipse of doubled size. They proved that the algorithm will finally find a path to t if s and t are connected. Also the number of steps of AFR is bounded by O(c2(p*)), where p* is an optimal path and c(p*) is the cost of that path. In their proof, they assumed the unit disk graph is a civilized graph. Finally they give a tight lower bound by showing that any localized geometric routing algorithm has worst-case cost O(c2(p*)).
Recently, Kuhn et al. [14] extend the Adaptive Face Routing to a routing algorithm called Other Adaptive Face Routing (OAFR). Instead of changing to the next face at the “best” intersection of the face boundary with st, OAFR returns to the boundary point closest to the destination. They proved the cost of OAFR is also bounded by O(c2(p*)) which is asymptotically optimal.
Greedy routing was used in early routing protocol for wireless networks. However, it is easy to construct a simple example to show that greedy algorithm will not succeed to reach the destination but fall into a local minimum, a node without any “better” neighbors. Then a natural approach to improve the potential of greedy routing for practical purposes is to combining greedy routing and face routing (or right-hand rule) to recover the routing after simple greedy routing fails in local minimum. Many wireless protocols used this approach [4], [9], [14], [12], [23] and [25].
Greedy Perimeter Stateless Routing (GPRS) [8] and [9] uses RNG or GG as the planar routing topology, then combines greedy and right-hand rule to forward packets in the network. It works as follows. When a node receives a greed-mode packet, it searches its neighbor table for a neighbor who is closer to the destination t. If there is one, it will forward it to that neighbor. When no neighbor is closer, the node marks the packet into perimeter mode. GPSR forwards perimeter-mode packets using a simple planar graph traversal (right-hand rule). When a packet enters perimeter mode, GPSR records in the packet the location Lp. Then when receiving a perimeter-mode packet, GPSR will first compare it with forwarding node’s location. GPRS returns a packet to greedy mode of the distance from the forwarding node to t is less than that from Lp to t. For more detail, please refer to [9] and [8]. GPRS can guarantee the delivery of the packets when the underlying network topology is a planar graph.
Recently, Kuhn et al. [14] proposed a new algorithm to combine greedy routing with their Other Adaptive Face Routing (OAFR). They called the new method Greedy Other Adaptive Face Routing (GOAFR). The idea is similar to GPSR. When greedy method falls in local minimum, GOAFR uses OAFR to recover the routing. Same as for AFR, they proved the cost of GOAFR is bounded by O(c2(p*)) which is asymptotically optimal. In addition, they show that the algorithm is also average-case efficient through extensive simulations. In [14], the authors showed simulations of a variety of face routing algorithms and their combinations with a greedy approach. Notice that unlike GPSR, when doing face routing in GOAFR, it does not return to greedy method until OAFR completely finishes the exploration of the face. This may affect the efficiency of routing. In [12], Kuhn et al. uses an “early fallback” technique to return to greedy routing as soon as possible. The new algorithm is called GOAFR+. It employs two counters p and q to keep track of how many of the nodes visited during the current face routing phase are located closer (counted by p) and how many are not closer (counted by q) to the destination than the starting point of the current face routing phase. When a certain fallback condition holds, GOAFR+ directly falls back to greedy mode. This modification makes an obvious improvement for the average case performance. Their theoretical analysis also proves that GOAFR+ is asymptotically optimal in the worst case.
We conducted extensive simulations to study the performance of our method compared with the previous method proposed in [1]. We compare them in terms of both the structure construction performance and the routing performance. We randomly put 500 nodes in a square with side length varying from 7 to 15 and the transmission range of each node is fixed to one unit. First of all, we want to know how many messages used by these two methods respectively. Fig. 5 illustrates a quasi-UDG graph with 100 nodes in a square region of 7. Fig. 6(a) and (b) show the virtual edges added during the process by priori art and our method. Fig. 6(c) and (d) show the final topologies generated by these two methods.
Fig. 5. A quasi-unit disk graph.
.jpg)
Fig. 6. (a) and (b): Virtual edges added by a priori art and our method; (c) and (d): final structure created by these two methods. (a), (c) Priori art, (b), (d) our method.
Our simulations show that our method uses significantly less messages than the method by Barriére et al. [1] for dense networks. The used messages are similar for sparse networks. Similar observation holds for the number of virtual links created: our method creates significantly less virtual links for dense graphs. See Fig. 7.
Fig. 7. Comparison of our method with previous method. (a) Virtual edges added and (b) messages used.
Notice that, a structure that can be constructed with less messages does not imply that the routing performance based on it is better than other structure. We continue to study the routing performances of the structures constructed by our method and by the method of Barriére et al. [1]. We test the Greedy-Face routing method on structures constructed by both methods (given the same original communication graphs). Surprisingly, we found that the routing performances based on these two structures are almost the same. See Fig. 8 for an illustration. We measured both the average route hops and average route lengths. Notice that, if a route uses a constructed virtual link, we have to measure the hops and lengths of the actual path stored at the end-points to connect them.
Fig. 8. Comparison of our method with previous method. (a) Average route hops and (b) average route length.
We consider a wireless ad hoc network composed of a set of wireless nodes
distributed in a two dimensional plane. Several protocols have been developed to
perform routing in ad hoc wireless networks based on the positions of the mobile
hosts. A typical assumption in these protocols is that all wireless nodes have
uniform transmission regions modelled by unit disk centered at each wireless
node. However, all these protocols are likely to fail if the transmission
regions of the mobile hosts are not unit disks due to natural or man-made
obstacles or weather conditions. In this paper, we describe a robust routing
protocol that tolerates up to roughly 40% of variation in the transmission
ranges of the mobile hosts. More precisely, our protocol guarantees message
delivery in a connected ad hoc network whenever the ratio of the maximum
transmission range to the minimum transmission range is at most ![]() . Our protocol saved the communication cost without
losing the performances compared with the previous method that can tolerate the
same transmission variance. Our simulations showed that our protocol
out-performs the previous method for dense networks significantly: it uses much
less messages and creates much less virtual links, while the routing
performances of our method are almost the same as the previous method.
. Our protocol saved the communication cost without
losing the performances compared with the previous method that can tolerate the
same transmission variance. Our simulations showed that our protocol
out-performs the previous method for dense networks significantly: it uses much
less messages and creates much less virtual links, while the routing
performances of our method are almost the same as the previous method. ![]()
[1] L. Barrire, P. Fraigniaud, L. Narayanan, Robust position-based routing in wireless ad hoc networks with unstable transmission ranges, in: Proceedings of the 5th International Workshop on Discrete Algorithms and Methods for mobile Computing and Communications, 2001, pp. 19–27.
[2] S. Basagni, I. Chlamtac, V.R. Syrotiuk, B.A. Woodward, A distance routing effect algorithm for mobility (dream), in: Proceedings of ACM/IEEE MobiCom’98, 1998.
[3] P. Bose, P. Morin, Online routing in triangulations, in: Proceedings of the 10th Annual International Symposium on Algorithms and Computation ISAAC, 1999.
[4] P. Bose, P. Morin, I. Stojmenovic and J. Urrutia, Routing with guaranteed delivery in ad hoc wireless networks, Wireless Networks 7 (2001) (6), pp. 609–616. Abstract-INSPEC | Abstract-Compendex | $Order Document | Full Text via CrossRef
[5] K.R. Gabriel and R.R. Sokal, A new statistical approach to geographic variation analysis, Systematic Zoology 18 (1969), pp. 259–278.
[6] D.B. Johnson and D.A. Maltz, Dynamic source routing in ad hoc wireless networks. In: T. Imielinski and H.F. Korth, Editors, Mobile Computing vol. 353, Kluwer Academic Publishers, Boston (1996).
[7] B. Karp, H.T. Kung, Gpsr: greedy perimeter stateless routing for wireless networks, in: ACM/IEEE International Conference on Mobile Computing and Networking, 2000.
[8] B. Karp. Geographic Routing for Wireless Networks, PhD thesis, Harvard University, 2000.
[9] B. Karp, H.T. Kung, Gpsr: greedy perimeter stateless routing for wireless networks, in: Proceedings of the ACM/IEEE International Conference on Mobile Computing and Networking (MobiCom), 2000.
[10] Y.-B. Ko, N.H. Vaidya, Using location information to improve routing in ad hoc networks, Technical report, Department of Computer Science, Texas A&M University, 1997.
[11] E. Kranakis, H. Singh, J. Urrutia. Compass routing on geometric networks, in: Proceedings of 11th Canadian Conference on Computational Geometry, 1999, pp. 51–54.
[12] F. Kuhn, R. Wattenhofer, Y. Zhang, A. Zollinger. Geometric ad-hoc routing: of theory and practice, in: Proceedings of 22nd ACM International Symposium on the Principles of Distributed Computing (PODC), 2003.
[13] F. Kuhn, R. Wattenhofer, and A. Zollinger, Asymptotically optimal geometric mobile ad-hoc routing, in: Proceedings of the 6th International Workshop on Discrete Algorithms and Methods for Mobile Computing and Communications (DIALM), 2002.
[14] F. Kuhn, R. Wattenhofer, A. Zollinger, Worst-case optimal and average-case efficient geometric ad-hoc routing, in: Proceedings of 4th ACM International Symposium on Mobile Ad-Hoc Networking and Computing (MobiHoc), 2003.
[15] X.-Y. Li, G. Calinescu, P.-J. Wan, Distributed construction of planar spanner and routing for ad hoc wireless networks, in: 21st Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM), vol. 3, 2002.
[16] S. Murthy and J. Garcia-Luna-Aceves, An efficient routing protocol for wireless networks, Mobile Networks and Applications 1 (1996) (2) Special issue on Routing in Mobile Communication Networks.
[17] V. Park, M. Corson, A highly adaptive distributed routing algorithm for mobile wireless networks, in: IEEE Infocom, 1997.
[18] C. Perkins, Ad-hoc on-demand distance vector routing, in: MILCOM ’97, November, 1997.
[19] C. Perkins, P. Bhagwat, Highly dynamic destination-sequenced distance-vector routing, in: Proceedings of the ACM SIGCOMM, October, 1994.
[20] S. Ramanathan and M. Steenstrup, A survey of routing techniques for mobile communication networks, Mobile Networks and Applications 1 (1996) (2), pp. 89–104. Abstract-Compendex | $Order Document | Full Text via CrossRef
[21] E. Royer and C. Toh, A review of current routing protocols for ad-hoc mobile wireless networks, IEEE Personal Communications 6 (1999) (2), pp. 46–55. Abstract-INSPEC | $Order Document | Full Text via CrossRef
[22] P. Sinha, R. Sivakumar and V. Bharghavan, Cedar: core extraction distributed ad hoc routing algorithm, IEEE Journal on Selected Areas in Communications 17 (1999) (8), pp. 1454–1465.
[23] I. Stojmenovic and X. Lin, Loop-free hybrid single-path/flooding routing algorithms with guaranteed delivery for wireless networks, IEEE Transactions on Parallel and Distributed Systems 12 (2001) (10).
[24] G.T. Toussaint, The relative neighborhood graph of a finite planar set, Pattern Recognition 12 (1980) (4), pp. 261–268. Abstract | Full Text + Links | PDF (469 K) | MathSciNet
[25]
Y. Yu, R. Govindan, D. Estrin, Geographical and energy aware routing: a
recursive data dissemination protocol for wireless sensor networks, Technical
report, UCLA Computer Science Department Technical Report UCLA/CSD-TR-01-0023,
2001. ![]()
.jpg) |
Kousha Moaveninejad received the Bachelor in Computer Soft Engineering from Sharif University of Technology, Tehran/Iran, in 1997. He joined the Department of Computer Science of Illinois Institute of Technology in 2000, as a M.S. student and received the Masters degree in 2002. He then continued his study as a Ph.D. student at Illinois Institute of Technology and his current research interests include wireless ad-hoc networks, computational geometry, algorithm design, and mobile computing. |
.jpg) |
Wen-Zhan Song received BS and MS from Nanjing University of Science and Technology in 1997 and 2000. He is currently a Ph.D candidate of Computer Science in Illinois Institute of Technology. He worked in telecom industry from 1997 to 2001 as a software system designer and team leader. His current research interest is mainly focus on network protocol and algorithm design, especially in wireless networks, sensor networks and Peer-to-Peer networks. He is a student member of the IEEE. |
.jpg) |
Xiang-Yang Li has been an Assistant Professor of Computer Science at the Illinois Institute of Technology since 2000. He hold MS (2000) and PhD (2001) degree at Computer Science from University of Illinois at Urbana-Champaign. He received his Bachelor degree at Computer Science and Bachelor degree at Business Management from Tsinghua University, P.R. China in 1995. His research interests span the computational geometry, wireless ad hoc networks, game theory, cryptography and network security. He is a guest-editor for MONET special issue on non-cooperative computing in wireless networks. He is a Member of the ACM, IEEE, and IEEE Communication Society. |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Volume 3, Issue 5 , September 2005, Pages 546-559 Data Communication and Topology Control in Ad Hoc Networks | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Copyright © 2005 Elsevier B.V. All rights reserved. ScienceDirect® is a registered trademark of Elsevier B.V. |